ΠΟΥ ΧΡΗΣΙΜΕΥΟΥΝ ΟΛΟΙ ΑΥΤΟΙ ΟΙ ΤΥΠΟΙ;

     Αυτή η ερώτηση είναι μια συχνή ερώτηση των μαθητών, ειδικά της δευτεροβάθμιας εκπαίδευσης,

όσων αφορά το μάθημα των Μαθηματικών. Όσο τα παιδιά πάνε Δημοτικό, μέχρι και Β΄Γυμνασίου, τα Μαθηματικά είναι απλά, πρακτικά και χρήσιμα για την καθημερινότητα, όμως από τη Γ΄ Γυμνασίου και ειδικότερα στο Λύκειο, γίνονται πιο σύνθετα και πιο αφηρημένα. Για τα υπόλοιπα μαθήματα , είτε τους αρέσουν είτε όχι, κατανοούν το λόγο της ύπαρξής τους. Στα Αρχαία, μαθαίνουν τη γλώσσα των προγόνων μας, στη Φυσική αναλύουν τα φυσικά φαινόμενα γύρω μας που είναι σχετικά απτά και εύκολα να τα φανταστούν, στα Μαθηματικά όμως τί γίνεται; Γιατί πρέπει να μάθουν την απόλυτη τιμή; Γιατί πρέπει να μάθουν να λύνουν παραμετρικές εξισώσεις β΄βαθμού, λογάριθμους και εκθετικές;
     Κι όμως, τα Μαθηματικά υπάρχουν γύρω μας, παντού, σε όλες τις επιστήμες και σε όλες τις εκφάνσεις της ζωής μας. Ας δούμε μερικά παραδείγματα για να κατανοηθεί η χρησιμότητα των Μαθηματικών:
   

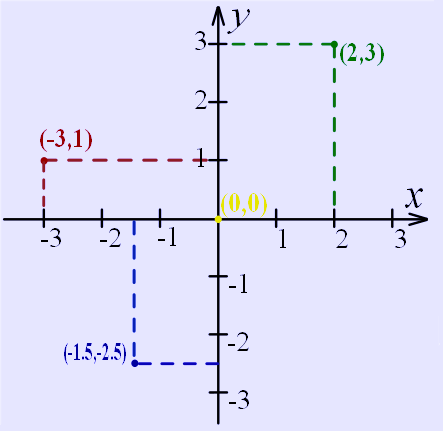
 Πώς θα μπορούσαμε να καθορίσουμε τη θέση ενός πλοίου αν δεν υπήρχαν οι συντεταγμένες και το καρτεσιανό σύστημα; Με τη βοήθεια επίσης της Γεωμετρίας μπορούμε να καθορίσουμε την απόσταση μεταξύ δύο πλοίων, δύο αεροπλάνων, προς αποφυγή συγκρούσεων, και γενικότερα δύο σημείων που είναι απρόσιτα.
      Τα Μαθηµατικά αποτελούν ένα από τους στυλοβάτες της ιατρικής επιστήµης. Οι  βασικές επιστηµονικές αρχές της στηρίζονται σε µαθηµατικά πρότυπα. ∆εν νοείται επιστηµονική σκέψη χωρίς τη θεώρησή της από µαθηµατική σκοπιά. Είναι αλήθεια για παράδειγµα ότι η ιατρική φυσική δεν νοείται χωρίς µαθηµατική υποδοµή.

ΜΙΑ ΓΕΩΜΕΤΡΙΚΗ ΕΦΑΡΜΟΓΗ ΣΤΗΝ ΙΑΤΡΙΚΗ
    Η έλλειψη είναι µία πολύ χρήσιµη και πρακτική κωνική τοµή. Το χαρακτηριστικό της είναι ότι το άθροισµα των αποστάσεων ενός τυχαίου σηµείου της από τις εστίες, είναι σταθερό. Μια άλλη

ιδιότητά της εξαιρετικά χρήσιµη, είναι η ανακλαστική. Η κάθετη στην εφαπτοµένη µιας έλλειψης στο σηµείο επαφής Μ διχοτοµεί τη γωνία, όπου E',E οι εστίες της έλλειψης. Σύµφωνα µε την ιδιότητα αυτή ένα ηχητικό κύµα ή µια φωτεινή ακτίνα που ξεκινούν από τη µία εστία µιας έλλειψης, ανακλώµενα σε αυτήν, διέρχονται από την άλλη εστία.
   Η µοναδική αυτή ιδιότητα της έλλειψης, ενέπνευσε τους επιστήµονες να κατασκευάσουν µια συσκευή για τη θεραπεία των νεφρικών και χολικών πετρών.

 Η ιδιότητα αυτή επίσης χρησιµοποιείται στο σχεδιασµό ορισµένων τύπων οπτικών οργάνων και στην κατασκευή των λεγόµενων "στοών µε ειδική ακουστική". Οι στοές αυτές είναι αίθουσες µε ελλειπτική οροφή, στις οποίες ένα πρόσωπο που ψιθυρίζει στη µια εστία µπορεί να ακουστεί στην άλλη εστία.
   Παρόμοιες εφαρμογές έχουν και οι υπόλοιπες κωνικές τομές, όσο ακαταλαβίστικες, δύσκολες και περίεργες και αν φαίνονται στη Β΄Λυκείου.


    Επίσης η Στατιστική, που είναι τομέας των Μαθηματικών, είναι ιδιαίτερα χρήσιμη στην ιατρική, προκειμένου να δουν, για παράδειγμα, το ποσοστό επιτυχίας που είχε ένα συγκεκριμένο φάρμακο σε ένα δείγμα ασθενών, για να αποφασίσουν αν θα συνεχίσουν να το χορηγούν ή όχι.
     Για τους ποδοσφαιρόφιλους, το ποδόσφαιρο, όσο περίεργο και να ακούγεται, σχετίζεται με τα

Μαθηματικά.  Οι θέσεις των ποδοσφαιριστών και οι στρατηγικές που ακολουθούν, μπορούν να αναλυθούν με τη βοήθεια των γραφημάτων και με θεωρία παιγνίων, που είναι τομέας των Μαθηματικών.
    Οι Μιγαδικοί αριθμοί έχουν άμεση εφαρμογή στο εναλλασσόμενο ρεύμα και χωρίς τις διαφορικές εξισώσεις δεν θα μπορούσαμε να υπολογίσουμε τις τροχιές των διαστημικών οχημάτων.Τα ορισμένα ολοκληρώματα, που υπολογίζουν εμβαδά συναρτήσεων, είναι χρήσιμα εργαλεία στους Πολιτικούς Μηχανικούς, στην Ναυπηγική, την Αεροναυπηγική και σε πολλούς άλλους τομείς. Οι Οικονομικές Επιστήμες, πώς θα υπήρχαν χωρίς τις παραγώγους, τη Στατιστική και τις Πιθανότητες;
 Τα παραδείγματα είναι τόσα πολλά που ένα άρθρο δεν θα έφτανε για να αναφερθούν και να αναλυθούν όλα.
 

     Τα Μαθηματικά δίνουν στους μαθητές κυρίως πνευματικά εφόδια. Τους βοηθούν να αναπτύξουν έναν τρόπο σκέψης πρακτικό και δομημένο. Αποκτούν κριτική ικανότητα και μαθαίνουν να αποδεικνύουν και να επιχειρηματολογούν. Συμβάλλουν στην πειθαρχία, τη σαφήνεια και την ορθολογική σκέψη, κάτι που οι έφηβοι δεν κατανοούν άμεσα αλλά σε βάθος χρόνου. Μέσω της Γεωμετρίας, της Στερεομετρίας και της Τριγωνομετρίας αναγνωρίζουν την αρμονία των σχημάτων της φύσης και κατανοούν τις ιδιότητές τους.
     Βέβαια όλα αυτά θα επιτευχθούν όταν στο μαθητή δε δοθεί έτοιμη <<μασημένη>> γνώση, παπαγαλίστικες στρατηγικές και συγκεκριμένες μέθοδοι, που με την παραμικρή αλλαγή δεδομένων ο μαθητής τα χάνει,  αλλά τα κατάλληλα ερεθίσματα ώστε να την ανακαλύψει μόνος του. Άλλωστε η βιωματική γνώση είναι εκείνη που μας μένει και την κατανοούμε καλύτερα, καθώς και η σύνδεσή της βήμα βήμα με προηγούμενες γνώσεις και με παραδείγματα από τη ζωή. Με αυτό τον τρόπο δεν θα έχουμε μία πιθανή επιτυχία στις εξετάσεις (Πανελλαδικές ή απλά ενδοσχολικές) με αποτέλεσμα μετά τις καλοκαιρινές διακοπές τα περισσότερα να ξεχαστούν, αλλά την ουσιαστική κατανόηση  και την ενίσχυση του ενδιαφέροντος των μαθητών για τη συγκεκριμένη επιστήμη.
    Στο πού χρησιμεύουν τα Μαθηματικά θα δώσω μια τελευταία απάντηση, σε μορφή ερώτησης, ως επίλογο του συγκεκριμένου άρθρου. Χωρίς τα Μαθηματικά τί θα υπήρχε γύρω μας άραγε;

Τζων Φορμπς Νας

Ο Τζων Φορμπς Νας (John Forbes Nash Jr.) (13 Ιουνίου 1928 - 23 Μαΐου 2015) Αμερικανός μαθηματικός και οικονομολόγος. Τιμήθηκε το 1994 με το Νόμπελ Οικονομικών, μαζί με τους Ρ. Ζέλτεν και Τζ. Χαρσάνυι για τη συμβολή του στη θεωρία παιγνίων. Συγκεκριμένα, δημιούργησε την έννοια της ισορροπίας για παιχνίδια μη-μηδενικού αθροίσματος, ισορροπία που πήρε το όνομά του ως ισορροπία Νας. Η έννοια της ισορροπίας κατά Νας είναι πολύ σπουδαία, ιδιαίτερα στις μέρες μας, και έχει ευρύτατες εφαρμογές σε πολλούς τομείς της ανθρώπινης δραστηριότητας, όπως στις οικονομικές επιστήμες, στην Πληροφορική, την Τεχνητή Νοημοσύνη, την πολιτική αλλά και σε φυσικά συστήματα, όπως η Βιολογία.

Το 2015, ο Τζων Φορμπς Νας τιμήθηκε με το Βραβείο Άμπελ μαζί με τον Λούις Νίρενμπεργκ “για τις εντυπωσιακές και σημαίνουσες συνεισφορές στη θεωρία των μη-γραμμικών μερικών διαφορικών εξισώσεων και στις εφαρμογές τους στη γεωμετρική ανάλυση”.

Ο Νας υπέφερε από σχιζοφρένεια από τα 29 του, την οποία ξεπέρασε μετά από τριάντα χρόνια.

O Τζον Νας και η σύζυγός του Αλίσια σκοτώθηκαν σε αυτοκινητιστικό δυστύχημα στις 23 Μαΐου του 2015, όταν το ταξί στο οποίο επέβαιναν προσέκρουσε σε προστατευτικό κιγκλίδωμα.

Νεότητα και αρχή της καριέρας του

Ο Νας γεννήθηκε στις 13 Ιουνίου 1928 στο Μπλούφηλντ, της Δυτικής Βιρτζίνια. Ο πατέρας του, ήταν ηλεκτρολόγος μηχανικός για την Επιχείρηση Ηλεκτρικής Ενέργειας των Απαλλάχιων. Η μητέρα του, Μάργκαρετ Βιρτζίνια Μάρτιν, απλά γνωστή ως Βιρτζίνια, ήταν δασκάλα πριν ακόμη παντρευτεί.

Μόρφωση

Και οι δυο γονείς του πρόσφεραν κάθε υποστήριξη στην εκπαίδευσή του, παρέχοντάς του εγκυκλοπαίδειες και επιτρέποντάς του να παρακολουθεί μαθήματα προχωρημένων μαθηματικών στο τοπικό κολέγιο, ενώ ήταν ακόμη μαθητής στο σχολείο. Η γιαγιά του Νας έπαιζε πιάνο στο σπίτι και ο ίδιος είχε μόνο καλές αναμνήσεις ακούγοντάς την, κατά τις επισκέψεις του στο σπίτι της.  Αφού φοίτησε στο Ινστιτούτο Τεχνολογίας του Κάρνεγκι (σημερινό Πανεπιστήμιο Κάρνεγκι Μέλον), από όπου ολοκλήρωσε τις σπουδές του, το 1948 με πτυχίο και μεταπτυχιακό μαθηματικών, έλαβε υποτροφία στο πανεπιστήμιο του Πρίνστον, όπου κυνήγησε την ακαδημαϊκή του καριέρα στα Μαθηματικά. 

Ακαδημαϊκή καριέρα

Ο πρώην καθηγητής του Πολυτεχνείου του Κάρνεγκι και επόπτης του Νας, Ρ.Τζ. Ντάφφιν, έγραψε κάποτε συστατική επιστολή με μία μόνο πρόταση: Αυτός ο άνθρωπος είναι ιδιοφυία. Ο Νας έγινε αποδεκτός και από το Χάρβαρντ, αλλά ο πρόεδρος του τμήματος των Μαθηματικών, Σόλομον Λέφσετζ, του πρόσφερε την υποτροφία Τζων. Σ. Κένεντι, που ήταν αρκετό για να θεωρήσει ο Νας ότι δεν εκτιμούσαν την αξία του.  Κατόπιν, πήγε στο Πρίνστον, όπου εργάστηκε πάνω στη Θεωρία της Εξισορρόπησης. Έλαβε το διδακτορικό του, το 1950 με μία διατριβή 28 σελίδων σχετικά με τα μη συνεργατικά παίγνια. Η θέση του, που γράφτηκε υπό την επίβλεψη του Άλμπερτ Γ. Τάκερ, περιείχε τον ορισμό και τις ιδιότητες, αυτού που αργότερα θα ονομαζόταν ισορροπία Νας.

Προσωπική Ζωή

Το 1951, ο Νας πήγε στο Τεχνολογικό Ινστιτούτο Μασαχουσέτης (MIT), ως καθηγητής του τμήματος μαθηματικών. Εκεί γνώρισε την Αλίσια Λόπες – Χάρρισον ντε Λαρδέ (γεν. 1/1/1933), φοιτήτρια φυσικής από το Ελ Σαλβαδόρ, την οποία παντρεύτηκε το Φεβρουάριο του 1957 σε μία καθολική τελετή αν και ήταν άθεος. Εισήγαγε τον Νας σε ψυχιατρική κλινική το 1959, μετά από διάγνωση σχιζοφρένειας. Ο γιος τους, Τζων Τσαρλς Μάρτιν Νας, γεννήθηκε σύντομα, αλλά έμεινε αβάπτιστος για ένα ακόμη χρόνο, καθώς η Αλίσια ένοιωθε ότι ο σύζυγός της έπρεπε να μπορούσε να εκφέρει γνώμη για το όνομα. Ο Νας και η ντε Λαρδέ έλαβαν διαζύγιο το 1963 αν και μετά την τελευταία και οριστική φορά που ο Νας έλαβε εξιτήριο το 1970, συνέχισαν να συζούν. Παντρεύτηκαν και πάλι το 2001.

Ο Νας ήταν για πολλά χρόνια κάτοικος του Ουέστ Ουίνδσορ στο Νιου Τζέρσεϋ.

H ταινία <<Ένας υπέροχος άνθρωπος>> αναφέρεται στη ζωή του Τζον Φορμπς Νας.

Πηγή: http://el.wikipedia.org/wiki/%CE%A4%CE%B6%CF%89%CE%BD_%CE%A6%CE%BF%CF%81%CE%BC%CF%80%CF%82_%CE%9D%CE%B1%CF%82 

Πολλοί πτυχιούχοι θα ήθελαν να έχουν γράψει χειρότερα στις Πανελλαδικές Εξετάσεις !

   Πολλοί υποψήφιοι πιστεύουν ότι αν γράψουν καλά στις Πανελλαδικές Εξετάσεις και περάσουν σε μία σχολή με υψηλή βάση εισαγωγής, θα έχουν  καλύτερες επαγγελματικές προοπτικές από εκείνες μιας σχολής με χαμηλότερη βάση. 

Αυτή η πεποίθηση σε αρκετές περιπτώσεις ευσταθεί αλλά υπάρχουν και πολλές περιπτώσεις που δεν ευσταθεί. Πολλοί πτυχιούχοι θα ήθελαν πολύ να έχουν γράψει χειρότερα και να έχουν περάσει σε σχολές με χαμηλότερες βάσεις. Ένας από αυτούς είμαι και εγώ.
Δεκαετίες τώρα οι βάσεις στις Φυσικομαθηματικές σχολές έχουν την εξής σειρά από την μεγαλύτερη προς τη μικρότερη: Βιολογικό, Χημικό, Φυσικό, Μαθηματικό.

  Όπως έχει αποδείξει η ζωή οι επαγγελματικές δυνατότητες έχουν την αντίστροφη σειρά! Ο

Μαθηματικός είναι ανάμεσα στα 10 καλύτερα επαγγέλματα στις ΗΠΑ εδώ και δεκαετίας και πολλές φορές είναι στη κορυφή. Πολλοί πτυχιούχοι υψηλόβαθμων σχολών (Νομικής, Φιλολογίας, Μαθηματικών, Φυσικών, Μηχανικών Πολυτεχνείων κπλ) πήραν δεύτερο πτυχίο από Παιδαγωγικό Δημοτικής Εκπαίδευσης (Δάσκαλοι/ες) για να διοριστούν στα Δημοτικά. Αξίζει εδώ να αναφερθεί η περίπτωση των πτυχιούχων πολυτεχνικών σχολών Ηλεκτρολόγων Μηχ/κων & Μηχ/κος Η/Υ, Μηχανολόγων, Πολιτικών Μηχ/κων, Τοπογράφων Μηχ/κων, Αρχιτεκτόνων Μηχ/κων πήραν και πτυχίο ΑΣΠΑΙΤΕ (πρώην ΣΕΛΕΤΕ) για να διοριστούν στη Δημόσια Δευτεροβάθμια Εκπαίδευση. Σύμφωνα µε τα αποτελέσματα έρευνας του ΑΠΘ το 2008, το 27,4% των αποφοίτων του Τµήµατος Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών (ΗΜΜΥ) απασχολείται στον τοµέα της εκπαίδευσης. (Η μελέτη: sep4u.gr/eng/HMMY.pdf ). 

Το να γίνει καθηγητής πληροφορικής (ΠΕ19) ένας πτυχιούχος ΗΜΜΥ, πολλές φορές με μεταπτυχιακά και διδακτορικά, δεν είναι και το καλύτερο σενάριο επαγγελματικής αποκατάστασης . Μπορούσες να πετύχεις το ίδιο ή και καλύτερο αποτέλεσμα με πολύ μικρότερη προσπάθεια. Αρκούσε να έχεις τελειώσει ένα ΤΕΙ Πληροφορικής ή μια άλλη σχολή που οδηγεί σε εκπαιδευτικά επαγγέλματα με (πολύ) χαμηλότερη βάση. 

   Πιστεύω ότι όλα τα παραπάνω να σας έπεισαν ότι η καλύτερη επίδοση στις Πανελλαδικές Εξετάσεις δεν είναι διαβατήριο για μια καλύτερη επαγγελματική πορεία. Εύχομαι σε όλους τους υποψηφίους καλή επιτυχία και να μην στεναχωρηθούν αν δεν γράψουν όσο θα ήθελαν. Κάθε εμπόδιο για καλό … ίσως.

Άρθρο από: http://sep4u.gr